我对国外励志片或者大家一致认为非常经典的电影从来不感冒,也一定是看着看着就会睡着了的人。 但是却熬夜看完了《当幸福来敲门》和《幸福终点站》,看完之后有一些觉得有趣的想法,我觉得写下来是一个不错的选择,写作其实是一种非常好的自我交流的方式。
我并没有对这两个电影表面的励志所感动,因为我从不怀疑一个人要得到某个东西的背后需要付出多大代价。我只是在静静地思考并汲取当一个人面对绝望,困境和无人倾诉的时候应当如何走下去? 有一个画面《当幸福来敲门》中父子二人因无法承担房租而流落街头,坐在地铁站台附近的长条凳子上一左一右,儿子突然看着Chris旁边的Box说道“Daddy Its not time machine...”, 直到看到这里时候我还在为这对父子如何渡过这个夜晚担心,我也以为Chris会尝试安慰儿子,但是Chris却说“Yes, It is...”,然后以此跟儿子做了一个小游戏回到了侏罗纪时代,把站台的厕所当做安全的cave渡过整个夜晚... 对啊Box为什么不能是time machine呢? 在那一刻它不是正好帮助了这对父子穿越了那片刻的苦难? 但是它却还只是一个Box。更让我觉得有趣的是,平时在生活总有许许多多的人,把自己困境当做祈求帮助的途径,而Chris并没有,它没有在找工作的时候告诉别人我是一个孩子的父亲,我们已经走投无路了,也没有在教堂排队等待分配临时住所的时候,因为自己还带着一个孩子希望别人同情一下,但是也看得出来他确实是一个自尊心很强的人。而在《幸福终点站》中整个机场对于Viktor就是一个Box,在这个Box某个角落67号登机口给自己建了一个家,结识了一些朋友,渡过了外人看起来不可思议的9个月。
我在想自己面对这些境遇的时候会如何做? 能不能拥有像Chris和Viktor一样的智慧?如果将Viktor在异乡的语言不通比作无人倾诉,Viktor无疑提供了一种比较好的方法,尝试找到共同语言,在尝试的过程中利用你可以接触的一切资源。这里有一个很自然的问题: 在我们的成长经历和日常生活该从哪里学习这种在困境中生活的方法? 这里我又想到了龙应台在《跌倒-寄K》中的一段话:
“我想说的是,K,在我们整个成长的过程里,谁,教过我们怎么去面对痛苦、挫折、失败?它不在我们的家庭教育里,它不在小学、中学、大学的教科书或课程里,它更不在我们的大众传播里。家庭教育、学校教育、社会教育只教我们如何去追求卓越,从砍樱桃的华盛顿、悬梁刺骨的张秦到平地起楼的比尔盖茨,都是成功的典范。即使是谈到失败,目的只是要你绝地反攻,再度追求出人头地,譬如越王勾践的卧薪尝胆,洗雪耻辱,譬如哪个战败的国王看见蜘蛛如何结网,不屈不挠。我们拼命地学习如何成功冲刺一百米,但是没有人教过我们:你跌倒时,怎么跌得有尊严;你的膝盖破得血肉模糊时,怎么清洗伤口、怎么包扎;你痛得无法忍受时,用什么样的表情去面对别人;你一头栽下时,怎么治疗内心淌血的伤口,怎么获得心灵深层的平静,心像玻璃一样碎了一地时,怎么收拾?”
没人教会我们,或者说别人也无法教会我们,因为有相同的经历才能让人共情。但是正如你所看到的Box is everywhere。 另外一个让我惊叹Box伟大的地方是modal logic里面出现的necessary modality, 第一次遇见它的时候是在natural deduction中作为characterize valid formula方式的出现,同时它又可以出现在lambda calculus中作为characterize closed term的方式。 但是它却只是Box,在见证了它无处不在,它最终以单独subsection named "Box is powerful"在我笔记里面存在。过去我不喜欢赋予冰冰冷冷的抽象事物以任何的感情,因为觉得它们永远只能那样,但是我逐渐发现它或许可以成为生活某个地方的钥匙。 直到我在姚期智大佬文中读到一个关于数学家保罗·埃尔德什(Paul Erdos)的故事:
“我想说的是他是完完全全一个专心做研究的人,而且他有一些特别的地方,他是没有家的人,365天,有360天在路上,在美国欧洲各个地方旅行,基本所需都在一个行李箱里,也不住旅馆,住在朋友家,基本都是数学家,从早到晚都可以交流。他有很多脍炙人口的小故事。比如Epsilon,微积分里用来代表“微小”,小(little)的意思,他喜欢用Epsilon代表小孩子。朋友问他:“吃过午饭了吗?(Have you had lunch?)”他回答:我吃了一点。(Yes,I ate an epsilon)。朋友笑他:你是食人族,吃了个小孩子! 再比如咖啡,他用一个词“定理咖啡(Theorem coffee)”来指咖啡很浓,可以激发数学思维,证明出定理。他在斯坦福访问时,曾在我们家住过两天,称赞储教授做的咖啡堪称“Theorem coffee”。他的整个思维,觉得数学不但是很高深重要的科学,也是社会合作的一个活动,觉得数学应该大家都参与,互相都合作,这是做数学最好的方式。科学界流行一个埃数(Erdos number)的概念,代表和Erdos合作的“最近”距离,可说是最早的一个社交网(social network)。网络之广,甚至许多生物学家、经济家都有一个近距离的埃数(Erdos number)。我本人的埃数(Erdos number)是2,这是因为储枫教授和埃尔德什(Erdos)教授写过一个论文,我又和储教授写过论文,所以她是1,我是2”。
显然Erdos教授将自己天天面对那些冰冷的东西以某种和谐的方式融入了自己的生活,为什么我不能呢? 在这里我也正式提出我的Box Theorem, that is, Box is everywhere! 如果将其称为The existence of Box, 那么我可以继而给出Semantic Box第二个定理Powerful Box Theorem, that is, Box is interpretable everywhere!
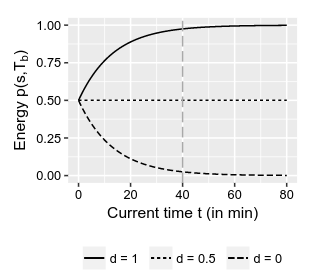
其实我想说是学会取悦自己是一个非常重要的能力,Box无疑是一种不错的工具,Box Theorem告诉你Box随处可见,而Powerful Box Theorem告诉你Box等待你探索它的意义。 但是并没有一个Deterministic Box Theorem告诉你某个Box一定有其特别的含义。 如果再将Box放到Kripke frame里面,Box此时会帮你记录下一个时刻会存在什么东西。 BoxBoxBoxBox... 盒中盒的形式也是存在的,至于它的语义不过是只是“人生无常,大肠包小肠”。
希望你也能找到自己的Box.
 如何插入phi
如何插入phi



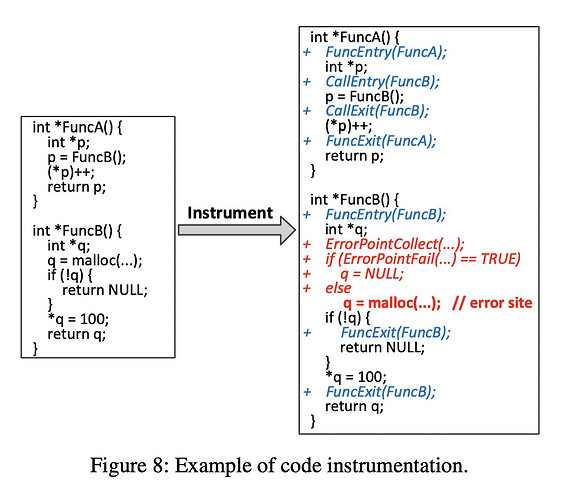
 采用上下文不敏感的方法在FuncP中的malloc注入错误,将会导致在调用FuncB时就直接退出了,而你就会错过调用FuncB而导致的double-free。试想有选择性地在FuncP的malloc中注入错误,将会有机会捕获到这个异常(第一个疑问when injects? )。
采用上下文不敏感的方法在FuncP中的malloc注入错误,将会导致在调用FuncB时就直接退出了,而你就会错过调用FuncB而导致的double-free。试想有选择性地在FuncP的malloc中注入错误,将会有机会捕获到这个异常(第一个疑问when injects? )。
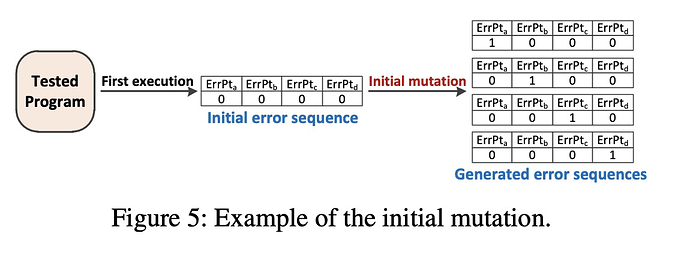
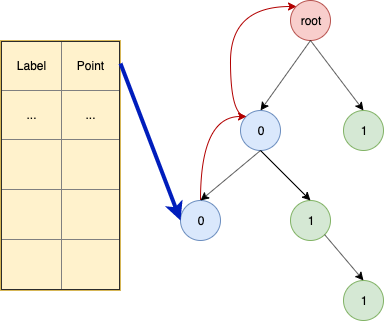
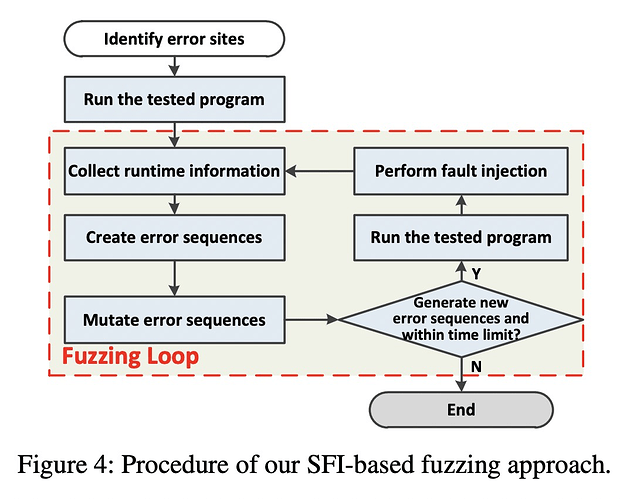 我从直觉上猜测的是,通过instrument标记error side,一次运行程序,得到可以被覆盖的error side,并不是简单的count,应该是有上下文敏感的count,通过得到这个信息,构造一个error sequence序列,表示应该去触发哪些error side。
我从直觉上猜测的是,通过instrument标记error side,一次运行程序,得到可以被覆盖的error side,并不是简单的count,应该是有上下文敏感的count,通过得到这个信息,构造一个error sequence序列,表示应该去触发哪些error side。