paper

directed-greybox-fuzzing

Directed Greybox Fuzzing

https://acmccs.github.io/papers/p2329-bohmeAemb.pdf

0x00 用一句话描述其内涵

directed fuzzer把大多数时间花在其关注的特定程序点上.

0x01 它能做什么呢？

  • patch testing 把关注点放到patch changelog上，更具体些即关注那些因为某处patch而改变过的代码，反过来去测试未打patch之前的应用。
  • crash reproduction 例如把关注点放到crash info的call stack上: 当一个crash report出现的时候，提供的有用信息可能只有相应的环境上下文，并没有特定的输入，这种情况下就make sense了，可能需要构造输入来触发相应的call stack来辅助探查问题。
  • static analysis report verification 顾名思义用程序真实执行结果来验证静态分析得到的相关结论，其过程也需要构造输入，构造的输入需要尽可能的往静态分析的结果位置走。
  • information flow detection 标注程序中的sinks和sources，作为敏感位置，为dynamic taint analysis提供驱动力。

0x02 现存相关的directed fuzzer存在的局限

  • 大多数based symbolic execution，被称为directed symbolic execution，它将reachability problem的求解过程转换为了一个迭代约束满足性问题（iterative constraint satisfaction problem）， ，其中表示某个已经已经reached的点，表示其reach到所需要的条件，接着你如果需要在的基础上探索更深的路径，你就可以考虑接下来需要的condition 。但是这样做就比较依赖source code，并且你需要构造对应某条路径的constraint，这里的constraint要作为可以求解的表达式，这就是说你需要一个constraint slover，太过于抽象不能转换为机器自动求解，也是鸡肋。当然你考虑在binary上来做的话也是可以的，只要你有相应的representation就行。
  • directed symbolic execution代价太昂贵，参考Katch；

0x03 简单介绍一下本文工作

本文在尝试改进directed fuzzer，在前提我们感兴趣的target side给定的情况下，我们如何让fuzzer的行进路线更优于它们？

  • 将reachability problem转换了一个优化问题，将种子和the distance of target side绑定来作为种子选择的依据；
  • 距离的度量分为过程间和过程内两个计算策略，其计算过程依赖call graph和control flow graph；
  • 距离的计算同时发生在静态（被compiler编译之前）和动态（程序运行之后），静态计算每个基本块与目标地址的距离， 动态计算种子的距离；
  • 在种子选择策略上使用模拟退火来驱动能量调度。

0x04 最值得关注点

  • seed distance的度量方式
  • seed optimization

0x05 seed distance的度量方式

1. function-level

用于度量某个给定函数和目标函数之间的距离，自然地这个距离的计算建立在CG(call graph)上。给定两个CG上的node 和，用表示它们之间的最短路径(shortest path)，路径的构成即CG上的edges。 最短路径的计算本文采用的是经典的Dijkstra算法。若给定某个CG上某个函数node 和目标函数构成的集合，对不同的目标函数你都要考虑最短路径，所以自然地的你要考虑在它们的基础上取平均，这里采用的策略是取调和平均(harmonic mean)。下面严格定义到的距离

其中表示那些对可达（reachable）的目标函数构成的集合，这里的undefined也可以理解为，意味着两者距离无限大。可以看到的是这个调和平均并不标准，大括号里面少了一个。这里为什么要用调和平均，而不是算术平均或者几何平均呢？实际上调和平均的哲学意义是如果一个过程中有多条平行的路径，经过这些平行路径之后，等效的结果就是调和平均。图中举了一个例子，用来解释算术平均对当前描述更近或者更远的路径这个意义下不是很敏感。

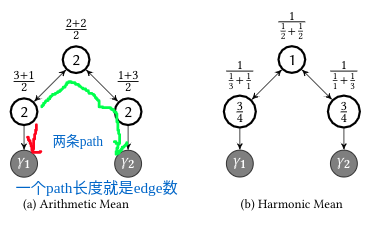
arithmetirc mean and harmonic mean

可以看到在算术平均下，三个nodes对目标函数距离的平均是相等的，这显然不符合预期。作为补充，文中更关注是找到一条最近的路径，这也可以成为什么选择调和平均的理由，因为调和平均和几何平均都是对小数更“敏感”，这个敏感如何精确的描述呢? 参考其图像，其中小数让其图像更陡(观察下图中变小的过程)，也就是说其描述的函数的二阶导是个负数。

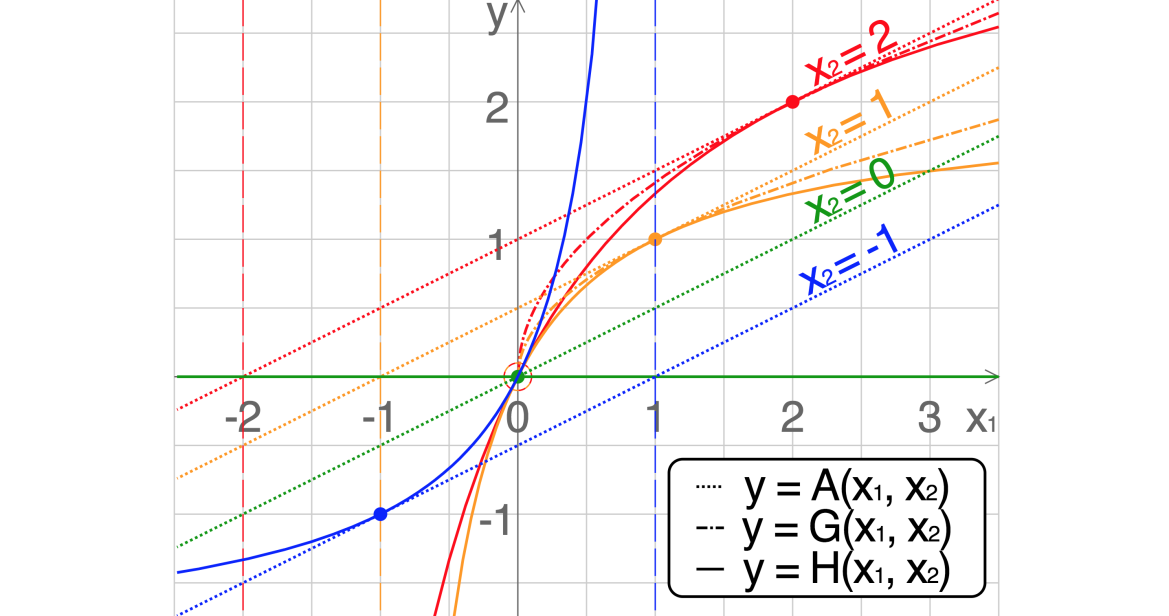
2. basic-block-level

用于度量给定某个基本块和目标基本块的距离。注意这个目标基本块它是指包含目标函数调用的基本块，也就是说文章的instrument过程不标记基本块为目标，而是如果某个基本块可能发生问题，我可以在这里插一个目标函数，让它往这里走. 给定某个特定过程内的CFG ，上某个基本块和目标基本块的集合，下面严格定义到的距离 其中表示基本块里面那些可以reach到的函数调用（间接或者直接），即我们有；表示上那些的所有基本块；是一个常量系数用于放缩函数间距离；表示一个CFG内两个基本块之间的最短路径，当然这两个基本块的路径可能是不存在的，这种情况下它们直接的距离可以描述为，这样在结果上也是well-defined。前述定义是足够清晰的，其涵盖的三种情况包括

  • 如果，正好落在了上，这种情况下自然和的距离为0;
  • 如果，那么取到目标函数最短的距离乘上某个常系数;
  • 在不满足上述两个情况的条件下，考虑在上可达的其他基本块，类似地考虑到的距离，同时加上到的最短路径.

实际上，针对前面计算操作，这里我有一个疑问是如何解决reachability问题？ 因为所有的计算都建立在假设已知函数和函数之间的可达性以及基本块之间的可达性的基础之上。关于这一点还需要去看代码才行。

通过前面定义的两种度量方式，我们可以在静态阶段就给某个CFG上每个node（基本块）都assign一个值，这个值就表示其距离目标函数的远近程度。然后利用这个值来计算当前运行过程中seed对应的seed distance，严格定义如下 其中表示某个seed，则表示执行所触发的trace，trace具体指在执行过程中触发基本块的个数。注意这里是取了一次算术平均，其合理性值得探讨，我猜可以从基本块之间的order关系展开。

0x06 seed optimization

在具体构建模拟退火调度之前，先理解文中提到的两个概念：

  1. exploration

    探索模式可以理解为在全局上有策略地随机的搜索最好的local解，这个过程aflgo和afl工作方式相同，都是基于覆盖率来调度seed sequence。这个模式要先于下面的exploitation，并不是一上来就基于user defined target info来做辅助，而是先拿到更多路径，到了一定limits再使用下面的策略，从直觉上说这是确实是对的，有了路径多样性，我们才能来做更准确的distance的测算。

  2. exploitation

    构造模式在前面探索模式达到一定limits就选择进入，例如设置相关的时间阈值。在拥有了路径的多样性之后，针对性对target location发起进攻，优先选择离target location更近的种子来进行fuzz，并增加其mutation次数。

exploration和exploitation由能量调度策略来进行切换，首先需要理解什么是the energy of seed？ 一个种子所带的能量其实就是指其fuzzer对其做mutation的次数，能量越大，fuzzer在其基础上产生的新种子可能就越多。

在“Coverage-based Greybox Fuzzing As MarkovChain”一文中使用了马尔科夫链来model fuzzing，结合power schedule来驱动fuzzing。本文作者正是由此而尝试使用模拟退火方法，因为模拟退火在本质上就是一种马尔科夫蒙特卡洛方法。常用于固定时间内在较大的解空间中搜索近似全局最优解的优化方法。模拟退火的思想借鉴于固体的退火原理，当固体的温度很高的时候，内能比较大，固体的内部粒子处于快速无序运动，当温度慢慢降低的过程中，固体的内能减少，粒子的慢慢趋于有序，最终当固体处于常温时，内能达到最小，此时粒子最为稳定。

模拟退火从描述是从某一较高的稳定出发，这个温度称为初始温度，伴随着温度参数的不断下降，得到近似解也在不断的变换。类比爬山算法，该算法每次都会从当前的临近解空间中选择一个最优的解，直到达到一个局部最优解。而模拟退火，即使某次搜索过程中得到了局部最优解，也有一定概率去搜索其他的解（接受非最优解），避免陷入局部最优解。这个概率是随着温度地降低而变化的，这个过程参照物理系统总是趋向于能量最低，但分子热运动则趋向于破坏这种低能量的状态，所以存在一定几率导致其能量并没有发送变化，温度越低这个概率是越小的。

在了解模拟退火的基本概念之后，首先需要model一个降温过程即cooling schedule，这个降温过程应该是比较缓慢的，文章使用model如下 其中通常定义为，为迭代次数，初始温度设置为。

前面提到exploration和exploitation切换的limits文章显式的设置为，求出为 注意这里用到是自变量迭代次数，这一值并不是直接的观察值，因此考虑用某一时间段来具体表示，让 ，其中作为某个设置好的limit time， 所有的seeds构成的空间就是我们这里的解空间，接下来就是model具体一个seed它的能量，在此之前首先要对做一个归一化（放缩），有点像模糊数学里面的隶属函数，即通过max-min的方法把放缩到，具体操作如下 其中，表示所有已知seeds构成的集合。

给定种子 和目标地址 ，在某一时刻，其能量model如下 我们先来简单看一下这个函数的性质:

  1. 这个函数在里面没有极值点，因此只需要考虑边界上的点. 当时，最大值为，同理当时，最小值为. 所以有.

  2. 对任意seed而言在初始状态时都相同的能量.

  3. 固定多个时刻，观察种子能量随着的变化，随时间增加越小，曲线越陡。

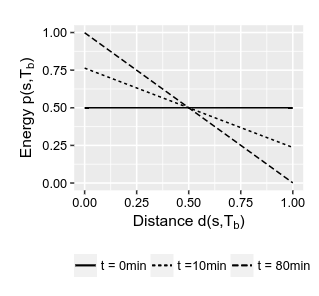
    energy under different timing

    相同时刻越小，其能量是越低的。

  4. 固定多个不同的种子距离，观察它们随着的变化

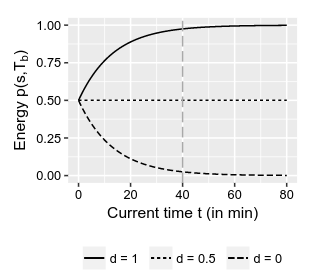
    energy under different seed

    这里很奇怪，时，这条曲线有问题，应该是随着时间的增加其能量也是逐渐增加收敛到，这里应该是和标注反了。

从图像上分析你会发现最终无论是随着时间或者种子距离都会其随着时间的增加而趋于稳定，这一点是至关重要的。有了R-value function 来model种子对应的能量，那么理想模拟退火的下一步是描述解是如何移动的，即model 如何接受新解？ 其过程可能通过和来model接受稍微差一点解的概率。但是文中下一步并没有这样做，因为在2.2b afl中已经有一个explore schedule机制了，文中的做法是对其schedule利用上面的进行二次调参，其过程如下 其中表示afl的explore schedule对赋值的能量。观察上述过程有下面的性质

  1. 前面我们分析的时候知道，在时所有seeds的能量都是，所以这里也有 这是符合预期的

  2. 由的最大值和最小值，可以得出的最大值为()和最小值为(). 符合越进近的种子，其能量是越大的。

整体上有一些definition我始终觉得缺点什么？

延伸阅读：

  1. Constraint-guided Directed Greybox Fuzzing usenix2021 （为target生成constraint，以slove constraint作为驱动）
  2. Targeted Greybox Fuzzing with Static Lookahead Analysis icse2020 （区块链但是它考虑targets的order关系）

参考资料：

  1. https://zhuanlan.zhihu.com/p/143016455 马尔科夫蒙特卡洛方法
  2. https://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html 大白话解析模拟退火
  3. https://zhuanlan.zhihu.com/p/47628209 比较详细和科学的模拟退火介绍