0x01 e-SSA Pis
在SSA我们经常能听见Phi,那么什么是Pi呢?,Pi就是一个特殊的Phi,它有range和constraint.,例如:
1 | if($a>5){ |
在路径条件的约束下,转头去执行不同路径分支时,某些变量就自动的满足了约束,但是有些情况我们是可以确定的,比如插入的第一个pi,但是第二个的phi的约束不一定完全正确,因为if分支可能影响$a的值。
php里面只考虑条件分支影响下的局部约束,记录一下几种特殊的约束法则的应用。
$a > 5很显然的约束$a + 5 == 0这里可以做一个变换$a = 0 - 5,分两种情况讨论即和 $a + 5 == $b +6同样这里也可以做变换$a = $b+((-5)-(-6))和$a+((-6)-(-5)) = $b. 这里的range除了constant还有其他变量的依赖. 这里为什么要写成上述的形式,我是按照php里面的计算方式来的,他会有一个操作数的adjustment,比如上面equal的RHS操作数的adjustment就是-5. 同理LHS操作数的adjustment是-6. 最后需要把$a和$b都单独表示表示出来,就需要adjustment之间做一下运算了.
上述提到的只是php中关于range的特殊约定格式,你也可以写出自己独特的约定。局部约束真的还是挺优雅的。
考虑几种情况不需要插
变量在target位置并不活跃,只用了一次,后面就不用了,我们在target位置插入一个
,没有什么意义. 依赖于incoming edge,如果有两条相同的incoming edge就不插,这是什么意思呢? 两条相同的incoming edge会无法区分pi是属于哪条edge. 但是我好奇什么时候会导致有两条相同的incoming edge,真奇怪? 还有一种非常特殊的情况,首先给一个definition: incoming edge定义为从'from'到'to',我们需要在to这里插入pi,我们考虑插入的pi目的是在to这里添加constraint,给我们后面的分析带来一些便利,但是可能你添加constraint是冗余的,举个例子
1
2
3
4
5
6
7
8
9$a = $b??$c;
/*
*1: T1 = ZEND_COALESCE $b,3
*2: T1 = QM_ASSIGN $c
*3: ASSIGN $a,T1
*/这里有3行opcode对应了三个blocks,第1行这里是可以尝试给第3行这里添加一个pi的,因为如果从第1行跳到第3行,那么
$b肯定不是null. 自然地我们可以在第3行这里添加一个pi断言$b不是null. 但是这没有意义,因为如果执行了第2行,那么第3行这里$b又是一个null,相当于之前添加的那个pi没有任何effort在这里起作用,即. 我们对 $b是什么还是一无所知.所以我们需要识别可能某个opcode造成的两种互斥的约束是否会merge,如果互斥的值同时可能流到to上,那我们去添加pi几乎没有任何意义的,幸运是,当前php的control flow相关的opcode都只有两个successors,所以我们可能不用考虑多个互斥的值同时作用.
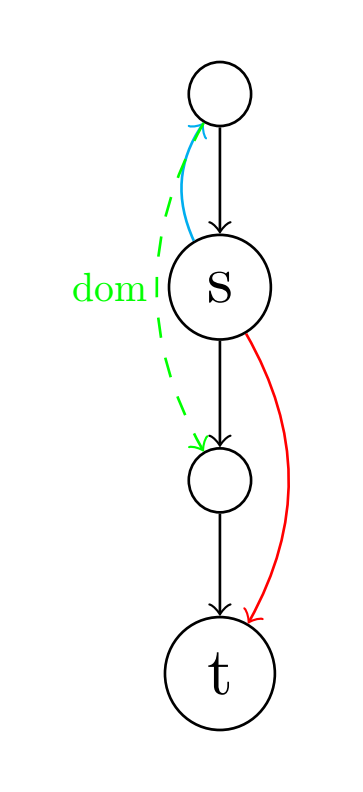
所以我们现在需要考虑from另外的successor(除了from到to的这条edge),我们记为other. 那么具体的问题是other到to是否有一条路径,并且这条路上,
里面constraint对应var没有发生变化? 其实这个问题回答其实是比较复杂的,因为找路径的同时你还要去关注var没有发生变化. php里面只做了最简单的优化. 记住我们在这里考虑要不要插pi,只是为了避免冗余的constraint,并不是说不能插,也就是说即使插了也是safe的. 所以尽量能减少多少算多少)php在这里会直接考虑to的直接前驱predecessor,如果predecessor里面的var发生变化了,不用想,经过这个predecessor都不会在我们的考虑范围之内了. 如果var没有发生变化,我们就要考虑other到这个predecessor有没有一条路径了,判断有没有路径最简单的方法就是看other是不是这个predecessor的dominator. (笑死!!!!) 再结合我们的问题下一步就显而易见了,有路径不插入pi, 实际上这个是不太准确的,我们在这里只知道有路径,但是路径具体是那条我们并不知道,并且在predecessor前面的路径上的节点var有没有发生变化,我们也是不知道. 所以这里只是作者的小推测. 其他我们没有提到的情况都会插入pi.
这里考虑如果插入的是prefect pi,那么它是真的有作用的. 如果插入是冗余的pi,这个constraint会造成一些错误吗?因为整个模式都偏向于不要插(留下这个问题,我要去看inference). 但是实际是要插入,而导致没有插入,将会导致后面inference的精度降低.
0x02 SSA Definition
- 在SSA表示下,任意状态下的某个变量使用,只有一个var definition能够生效。
- 程序的控制流在SSA下保持不变。
- 有一个特殊的merge操作
,用于处理多个前驱node的变量definition的交汇取值。 - 并不是所有node交汇处都需要
。 - 自然地如果在交汇处所有前驱node对某个变量的definition都相同,则不需要使用
。 - use-def analysis is faster on SSA (application)。
- SSA to machine code i.e code generation
如何精确的插入phi呢?
single reaching-definition: A definition
直觉上如果有两个distinct 基本块
Join Set Definition 给定图上的节点集合
给定
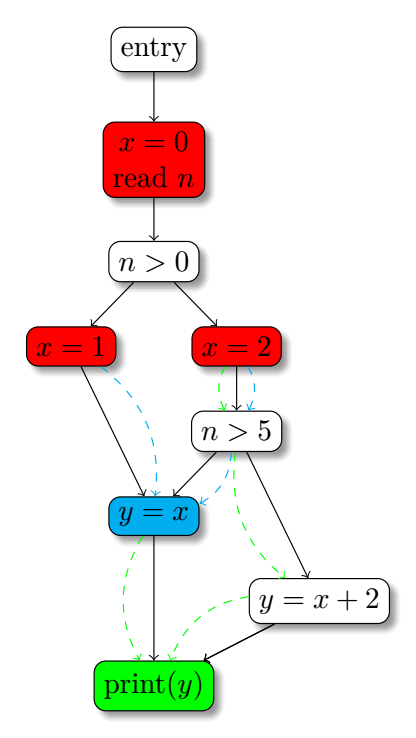
那么如何让插
如何插入phiDefinition 给定某个结点
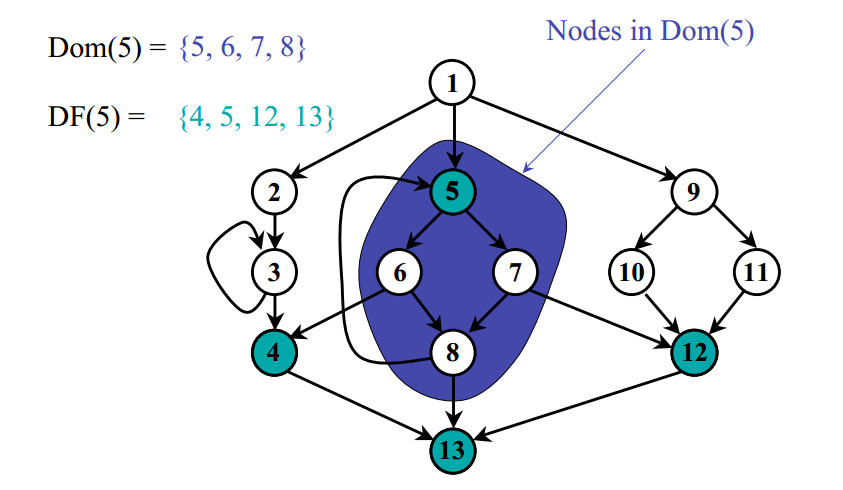
为什么dominance frontier可以帮助我们解决在哪里插入
那么如何计算

这算法很神奇啊,从每个结点
首先这个算法并不是一开始就对某个
点寻找它的df,而是在确定 是谁的df? 所以算法一开始从 的前驱开始。 因此考虑每个前驱
结点,从 在dominator tree向上回溯,得到结点序列 都是严格支配 ,所以这个结点序列任意一个结点 到 的所有路径上都有 支配 的,接下来只要保证 不支配 ,那么 ,这也是上述while循环中的条件. 这里也需要一个小lemma,dominator tree上的路径并不是CFG中的真实路径:
dominator tree上任意两点
, , 如果他们之间有一条路径, 不失一般性假设 的level小于 的level,那么也可以在CFG上找到一条 到 的路径,且 支配这条路径上的所有结点。 proof: 假设不存在这样的路径,即所有这样的路径,
都不完全支配其上的所有点,那么总可以找到一条从start不经过 到 的路径,这和 dom 是矛盾. 所以原命题得证。
还有一个小问题,为什么可以保证一定可以碰到
就是 的 . 这是trivial的 - 如果
不是 的 ,我们需要证明 也必须是 的dominator,假设 不是 的dominator,则存在一条经过 不经过 的路径抵达 ,产生矛盾了 不支配 . 所以 是 的一个dominator,所以往上回溯总可以碰到 .
0x03 SSA Construction
变量声明周期的维护,保证runtime阶段所有definition reachable且任一程序点某一时间点只有一个definition起作用. 每个变量只有一次的赋值机会,即每次assignment的左端的变量名都是独一无二的,保证definition的唯一性.

这个算法看起来也很简单,先收集所有的变量
直觉上是ok的,所有变量

让我们来推理一下这算法这背后的直觉?
这个过程里面糅杂了reachingDefinition的东西,这玩意儿就是一个definitions cache,也正是我们处理
这个reachingDefinition作用是什么呢? 注意在上述在处理def-var的时候,会把一个变量老的definition和新的definition用一张链表串起来. 那么reachingDefinition的作用就是你想在某个instruction处使用某个变量,它会准确地帮你找到这个变量的定义,如何描述“准确”呢? 就是离这个instruction最近的关于对应变量的definition,“最近”表示某个变量definition所在的基本块是dominate当且使用这个变量的基本,且这个definition所在的instruction离当且instruction在线性距离上最近(closest definition that dominates i). 你也理解为先在当且基本块找definition,找不到再去idom,具体操作见下图. reachingDefinition会帮你管理好这样一条def-chain,其中v.reachingDef就是一个链表元素。

一些细节问题:
为什么要深度遍历dominator tree?
我们目的是给每个assignment的左边重命名,再把assignment右边的变量名再修正. 所谓重命名就是给某一变量在重新被赋值的时候,给变量名加了一个下标,这个东西叫version. 为了控制version我们需要有序东西存在,采用dominator tree先序遍历的原因:
- 可以保证在处理每个基本块的Phi的时候,Phi里面的source var已经被重命名了.
- 让reachingDef chain works.