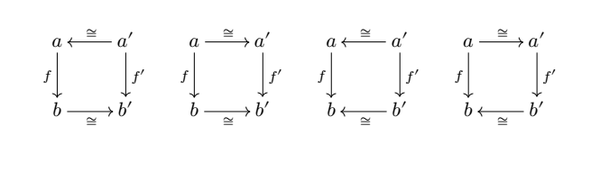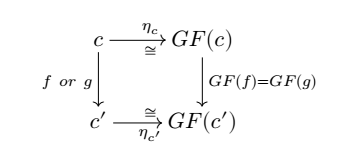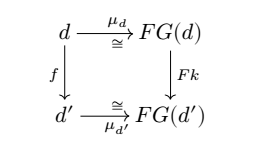定理1.1. 如果一个函子是等价的，当且仅当这个函子是faithful，full，essentially surjective on objects(dense)。
在证明这个定理之前，需要提出一个小lemma
引理1.2. 对于态射 和同构 , 可以唯一确定态射 ,等价地下面四个交换图
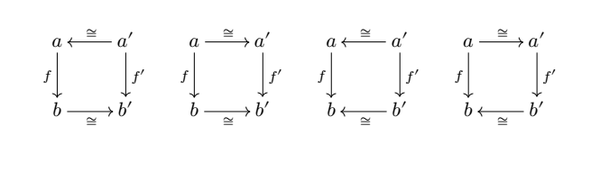img
从这几个交换图上我们已经很容易构造出 了,简单描述一下，定义 和 ,反之它们的逆用 和 表示。第一个最为直观
开始证明定理1.1 给定 ， ， ， 定义了一个范畴间的等价关系。对于任意的 ，有 ，取 ,显然 是稠密的。再考虑两个并行的态射 ,如果 ,则 和 同时满足下面交换图
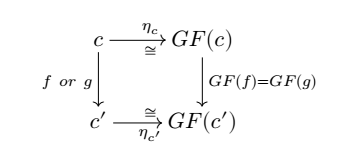img
根据引理1.2， 是唯一确定的，所有 ,因此 是一个局部单.对称地，考虑 和同构 ， ,可以唯一确定
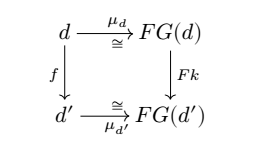img
,所以 是局部满的。
这个方向证明，我在怎么用dense这个性质的时候想了很久，最后突然发现一句“由选择公理”就完了，就完了，是的，你没有听错...
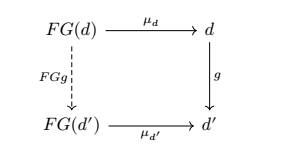
任取 ，由dense性质和选择公理,是可以构造一个 ,在dense下选一个 让 .对象映射处理好了，就可以来构造一个交换图了
img
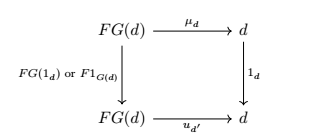
任取范畴 中一个态射 , 和 都是同构，所以可以上面的lemma可以唯一确定一个 。因为 是faithful，所以换个角度看 也是唯一的，现在 里面所有的components都是可以确定一个交换图的，且都是同构的，但是这里有一个问题，我们用选择公理弄了上面这样一个 出来，我们并没有证明它确实是一个函子，还少一步验证它对态射作用，首先是单位态射，我们有下面这个交换图
img
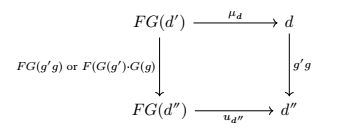
还是由前面的lemma和 上对态射的单射性质，这里有 ,相似地，再给一个态射 ,我们有下面的交换图
img
这里有 .
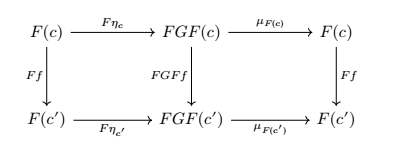
现在已经完成了前一半的证明，接下来想一下如何构造 .并不能直接来构造，尝试构造下面的交换图
img
声明一下其中的几个定义，态射 ,两个component , ,把 定义为 . 这样做的目的是使得 再反过来做一次就得到了同构 .
再看这个大长方形和两个小正方形的交换性，大长方形由上述定义交换，右边这个小正方形因为 是个自然同构，所以也是交换的，言下之意左边这个小正方形也是交换的。这两个小正方形带来的作用是什么？左边这个交换可以得到
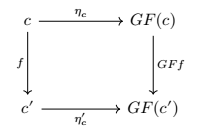
再由 的faithful性质，即有 ,这个等式就表示下面的图交换
img
乎将近拖了半个月的证明，终于证完了，选择公理的应用和间接构造自然同构，还是得在细细想想...