php optimizer about identifying loops

这篇文章用于记录php optimizer中关于循环结构识别算法，看了一些php optimizer components，目前最大的感受就是一个component一篇论文，每一个component都有它的出处，你如果单看代码，你很难去读懂它在描述怎样一种算法，所以你必须去看它出处的论文，只有读懂论文以后，你才能抓住最本质是东西去套代码。很幸运我遇见了正在“高速”发展的php，我很珍惜跟随着这些写optimizer的developers去学习的机会，php里面几乎%90的optimizers都是dmitry写的，我真的很佩服他...

我最近的工作中也需要identity loops的协助，有向图中循环识别算法很多，php里面用的算法来自于

Identifying Loops Using DJ Graph

这篇论文构造了一种叫DJ图结构去辅助识别循环，DJ图到底是什么呢？其实用特定的flowgraph生成的dominator tree(支配树)的基础上，把原flowgraph的边(不在dominator tree 中)以join edge的形式又添加到了dominator tree上，就构造了所谓的DJ图，这里J就是指的join edge。

Definition: 是flowgraph上的一条边，如果, 则称边是一条join edge。

这里我们引用论文里面的图，来具体的理解一下：

img

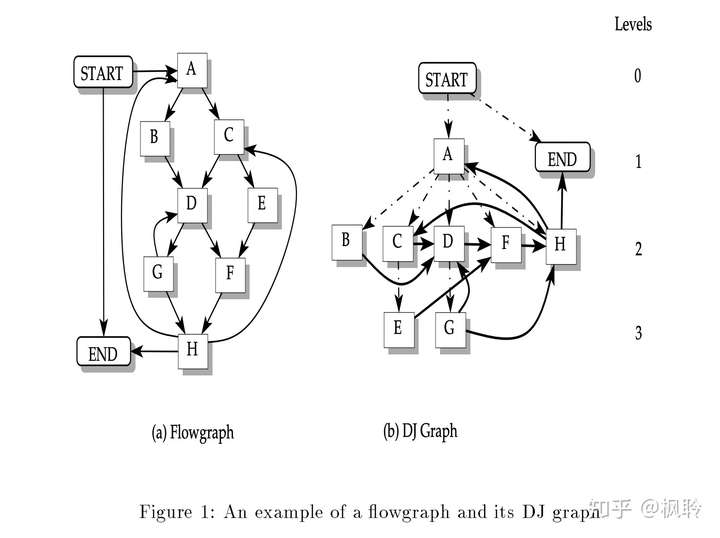
图a是原flowgraph，图b是生成的DJ graph，其中虚线是原flowgrpah的dominator tree上的边，而黑体实线就是join edges。

介绍完了关于DJ图构造，现在需要稍微了解一下关于循环的定义，循环也是有两种具体分类：

• reducible loop

  从循环最本质的直觉上，循环开始叫loop header(循环头)，在reducible loop里面这个loop header是唯一，且是严格支配其loop body(循环体)里面所有的节点。

  当然还有更一般的定义，reducible loop 也是指单入口强连通分量。reducible loop也关系到flowgraph的可约性，如果一个图是可约的，当且仅当我们可以对它的边划分为两个disjoint groups：

  • forward edges ：所有的forward edges里面的边，可以构造一个无环图，且所有图上的点和root节点都是可达的。
  • back edges：所有的back edges里面的边，目标节点支配源节点，即，

• irreducible loop

  irreducible loop 我们可以使用暴力的手法，不是reducible loop的其他循环都是irreducible loop （很多定义都是这样，但是出奇的好用，哈哈）

有了关于DJ图和循环的基本概念，尝试理解为什么DJ图能辅助识别原flowgraph里面的循环？

我们对dominator tree引入的J边构造了DJ图，可以看到DJ图上也有循环，现在我们还不知道这个循环是不是和原flowgraph是一一对应的，但是我们在尝试关注循环的时候，常常关注一种特殊的edge，称之为back edge，狭义上的理解就是把一条长而直的路径，突然把头和尾连起来变成了一个环。这种定义还是很模糊，我们尝试把这样的边放到DJ图上去，这样边肯定属于J边了，不可能是dominator tree上的边。现在给出严格定义：

Definition:将J边分为两种类型的边: Back J(BJ) 和 Cross J(CJ).

1. 若一个J边是BJ边，则 dom
2. 不是BJ边的其余边都是CJ边

BJ边就是我们环里面很重要的一类边，但是我们需要验证一下DJ图上的环和原flowgraph的环是不是一一对应的？

如何证明呢？其实不用证明只要保证原flowgraph上的边都在DJ图上出现了即可，哈哈 有趣。但是呢DJ图因为dominator tree的原因加入了一些在原flowgraph不存在的边？这些边会有什么副作用吗？实际上并不会，你看见似乎引入了很多新环，但是其实我们关注的只有BJ边，BJ边都是实际flowgraph存在的边。

上面把DJ图和原flowgraph的关系理清楚了，那么我们具体是怎么识别环的呢？

一个自然循环在flowgraph里面有循环头和循环体，例如常规的while，for等等，但是也有那么不太自然的循环，例如用goto来构造一个循环，常规的循环其实就是reducible loop，而用goto你就有可能搞出来irreducible loop，前面已经提到了，在reducible loop里面循环头是严格支配其循环体所有结点的，所以只要把每个reducible loop header弄出来，就可以唯一确定一个reducible loop。但是irreducible loop没有这个唯一的循环头啊，怎么办呢？为了和reducible loop识别方法统一，我也要给irreducible loop加一个header，但是这个header不唯一怎么呢？还有办法，对DJ图做一次深度遍历得到一个生成树，在生成树上那个最前面的那个header，我们作为irreducible loop的header。

值得一提是这里有一个小lemma，即使irreducible loop的header不唯一，但是它们都有一个唯一的idominator，这个lemma证明很简单，只需要用反证法假设有两个idominator即可证明，Sreedhar的论文中有详细的过程。

下面是在php中的具体应用：

前置工作我们需要的是一个dominator tree，还需要一个DFS spanning tree(深度优先生成树)。在这里php并没有生成一个生成一个显式的spanning tree，而是很聪明地使用entry/times的方式记录深度遍历过程中节点与节点的关系,可以理解为一个拓扑路径： A_entry，B_entry，B_exit，A_exit，这样就相当于B是A的子孙节点，不需要生成完整的spanning tree原因是，我只需要在识别irreducible loop的时候，查询loop header之间的祖孙关系，去唯一标识一个header即可。

找loop header是从DJ图的最下面往上找的，这个可以根据dominator tree level进行排序，具体过程我可以用一个简化的算法表示：

for (n = 0; n < cfg->blocks_count; n++) {
	n = sorted_blocks[n].id //sorted_blcokeds 里面已经是从dominator level 从高到底排好了基本块
	for (j = 0; j < blocks[i].predecessors_count; j++){ //所有的入度边
		if (blocks[i].idom == pred) { //我们只关注J边
				continue;
        }
        
        if (dominates(blocks, i, pred)) { //当前bb支配前驱节点，也是我们说的BJ边
       		//这里就是标记reducible loop的位置  
        }else{
        	if (entry_times[pred] > entry_times[i] && exit_times[pred] < exit_times[i]) {
        		//不是BJ边，我们只标记在spanning tree里面那个bb为循环头 
        		//这里就是irreducible loop
        	}
        }
	}
	//...
}

有了循环头之后，之后就是把循环体对应到循环头上，这里面需要考虑循环嵌套的过程。所以每个bb只关联离他最近那个循环头。

呼，洋洋洒洒写了一些东西，我记性不好，写下来以后忘了看看，不然觉得挺可惜的。后面有时间我也许可以记录一些php里面其他optimizer的东西。如果有人看的话，看看就行，因为很多也是我胡诌的，哈哈。