paper

Matryoshka:Fuzzing Deeply Nested Branches

0x00 Questions

这篇文章意在解决“嵌套”的条件结构（注意这里的嵌套并不是狭义上控制结构嵌套），这是一个比较难处理的问题，在找到一个能触发新分支 的输入 ，接下来的策略肯定就是在这个输入 上，去构造新的输入 来触发更多的新的分支，但是这里面有一 个问题，假设新分支 内有一个子分支条件是 ,这个分支条件位置为 (reachable by ),那么分支 的子分支就可以抽象为 ,构造出来的输入 ,极有可能 点并不是reachable，因为可能 点之前的某个分支条件满足性，在输入 和 上并不相同:

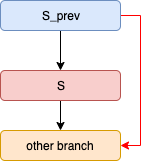
matryoshka

这里通过一个代码片段，来特别地说明几种特殊的情况：

image-20201003200124109

控制流依赖，L6依赖于L2，L3，L4。（这里的依赖对象是分支条件，下同） 数据流依赖，L6依赖于L2，L3。

如果我们想要进入L6的true分支，首先(1 L6 is reachable，（2 satisfies L6’s condition。

0x01 The ways

1.1 分支条件的控制流依赖

这个依赖可以看作是从CFG上剥离出来的东西，图上的点从基本块变成了分支条件，什么是分支条件？可以更具体一点，cmp/jmpz(nz) 等等的组合，为了把分支条件之间的关系，描述更加紧密，文中抽象了一个叫prior conditional statements 的概念，对一个指定的路径条件 ,它的prior conditional statements是可能导致 变成unreachable的一组路径条件。

这个定义在实现过程中还是比较抽象，需要具体的研究一下它的性质，首先考虑它并不是一个等价关系（不满足对称性），那么它是一个偏序吗？自反性很显然，传递性也很显然，反对称性呢？考虑两个不相同的路径条件是否相互为prior conditional statement ,这个不要去想的太复杂，在这篇文章描述的依赖关系下，是不可能做到，因为执行流，两个statements，肯定有一个是先执行的。

抛开反对称性不说，重点关注它的传递性，这里prior conditional statement 关系我用 表示。传递性可以描述为 为了找到指定路径条件 所有的prior conditional statements，可以使用这个性质，但是还需要定义一个immediate prior conditional statement,如果 是 的一个immediate prior conditional statement,则在 和 之前找不到第二个prior conditional statement,这个“之前”是指所有执行到 到路径，往后看 都是最后一个路径条件。可以简单的理解为 离 最近。这个定义对研究路径的同学来说，是非常熟悉的，就是dominator tree的定义，仿照它的定义，是可以给出计算prior conditional statements的算法的。 其中IPrior表示immediate prior conditional statement

通常来说dominator tree只定义在过程内，文中又进一步改进，引入了过程间的prior conditional statement 关系，这个也很好理解，如果一个路径条件 在过程内没有prior conditional statement,那就去找调用个过程的call的prior conditional statement，这里会产生一个疑惑不是描述路径条件之前的关系吗？怎么又突然来了一个call，按照定义描述的是“可能导致这个call 变成unreachable的路径条件”，其实是合理的。

我以为文中技术实现是完全建立在静态分析上，但是直到读到这里，trace和stack的出现，告诉我极有可能是在动态过程中做的，而且文中给的找immediate prior conditional statement的算法是可以在动态做的。

Intraprocedural immediate prior conditional statement：（ of ）

  • 和 s在同一个函数内

  • 不是 的 post-dominator (post-dominator ：如果 到exit -point的所有路径都经过 )

Interprocedural immediate prior conditional statement（ of ）

  • 和 不在同一个函数内
  • 当 执行的时候， 的返回地址在当前的栈中。
  • 是 执行过的最后一个调用， 不是 的post-dominators

文中还提到的路径分支包含terminator的情况，其实这种属于上面第一种情况了，因为第二个条件已经限定了。但是作者在这里还是特别的拿出来说了一下，我还是在这个放个小例子：

1
2
3
4
5
6
7
if(x==1){
  exit();
}

if(y==2){//target
  //...
}

1.2 分支条件的数据流依赖

用 表示流到分支条件 上的input bytes集合， 表示一个或者多个分支条件。当input在 处可达，为了进入 代表的分支，需要进一步修改input, 在修改之后， 里面路径条件选择不变的情况下， 还是reachable，从直觉上来说，为了尽可能小的影响 里面的路径条件，需要尽可能的避免修改 的input bytes,但是这样做有可能带来负反馈，例如F2中 ,这将直接导致根本无法进入L6所代表的分支。

这种情况下只考虑了分支条件的控制流依赖，并没有考虑路径条件之前的数据流依赖，这里文中又定义了第二种关系effective prior conditional statements ,我们需要稍微去改变一下上面我们的直觉，先忽略考虑reachable，我们需要改变 里面涉及到的input bytes ，改变这些input bytes 意味着 里面和它相关的路径条件的选择可能就会发生变化，我们需要尽可能保证他们的选择，所以应该去重点修改 ,很显然在这里 。这个直觉要比第一次的直觉要好那么一点点，但是也有问题，例如F2中 , ,所以 . 这个直觉在Matryoshka中是第一个求解约束的策略Prioritize reachability

1.3 求解约束

前面已经提到求解约束的一个策略，在这里需要综合考量reachable 和 satisfy constraints ，文中在这里提出了三种可选的策略，顺序执行：

  1. Prioritize reachability
  2. Prioritize satisfiability
  3. Joint optimization for both reachability and satisfiability

1.3.1 Prioritize satisfiability

这个策略非常有意思，修改 之后可能导致 变成unreachable,但是强制使 里面的路径条件选择不变（运行时），这个过程叫forward, 当在某次修改input之后，满足了条件,结果有两种：(1 如果 中的路径条件选择并没有发生变化，代表 成功了 （2 如果 中的路径条件选择发生了变化，则需要修补发生改变的路径条件，进入backtrack过程。

bracktrace过程从 向后按顺序fuzz 里面的每个路径条件 ,这个过程中需要避免修改流入 或者在 后面的effective prior conditional statements的input bytes,bracktrace成功的标志是处理完所有EPrior(s)的路径条件。

还是用F2中的例子来说明问题：假设当前的输入为 , L2,L3是L6的effective prior conditional statements，L2和L3下进入都是true分支，目标是进入L6的true分支，在修改 关联的input bytes过程中，强制使L2和L3也保持true分支,假设 ,满足了 但是L3选择是false，所以进入bracktrace过程，继续slove L3，这个时候需要避免动 的值，当 的时候，就找到一组满足L6的input bytes.但是这里如果在一个forward过程中选择了y=3,就直接导致后面的bracktrace失败了。

1.3.3 Joint optimization for both reachability and satisfiability

总结一下，Prioritize reachability旨在修改那些不会影响EPrior(s)的input bytes，保证 是reachable，Prioritize satisfiability使用forward-backtrace方法，尽可能的满足 .但是它们都可能在尝试优化多个路径条件的时候失败。这里文中通过对Angora的梯度下降算法再改造：

  • 表示 中每一个路径条件的黑盒抽象函数，同样使用和Angora一样的转换表：
image-20201004163325349

  • 其中 相当于一个max函数， 二元运算符表示取最大的那个操作数，并用 表示 的抽象运算。观察这里转换表比Angora多了一个 ,用于区别路径条件类型的最小正数。当 的时候，必然有 , 在这里把 作为预期最优解。（我觉得应该是 ,如何保证每个 这个事实？）。需要注意的是它这里要比Angora做的更好，因为Angora在计算偏导数的时候，并不能保证 是reachable，这样得到的结果没有意义，Angora面对这个问题，只是简单提到了通过改变单位分向量的值。这里Matryoshka可以强制保证previous分支选择，来保证计算过程。

    同样这样也用F2中的例子来说明问题，让 为初始 ： 通过梯度下降，最终会得到一个solution 为

1.4 隐式条件路径

直接用例子来说明问题： image-20201004184742827

L6计算显式的 ,很显然L3应该是属于 的，但是现有的方法是无法把它区分出来的，针对这种类似隐式的污点传递，通常的做法是如果路径条件被污染，则把该分支下的所有赋值操作都视为污点传递。这种方法文中提到，可能会导致over taint 和 taint explosion 。（但是我认为这样做理论上并没有问题，例如L4中n也被tainted,作者认为是useless，就算它是useless也不会影响其他的东西，考虑到因为这些污点导致更深的传递过程，也是合乎情理的，这属于一种indirect tainted,我猜测处理它的难点在于与之关联的input bytes不好做对应，这个过程需要手工的添加一些额外的taint rule）

作者并不想按照通常的手法来操作，而是通过相关的策略把隐式污点过程筛出来：假设当前的 对 是reachable的，但是经过mutate以后变成unreachable了。再额外运行两次，第一次记录original input过程中经过的路径条件，第二次记录mutated input过程中经历的路径，但是这个过程强制进入original input的路径选择，使其变成reachable,这两次得到的路径条件序列应该是相同的，按时间倒序检查它们的路径条件序列。

如果存在一个 ,并且 前后两次路径选择并不一样，则有可能存在与 的隐式路径依赖，需要进一步做验证，再跑一次mutated input，并且强制针对下面的路径条件和original input做到统一：

  • 所有在r之前的条件路径

  • 所有显式的effective prior conditional statements

  • 所有已知的隐式的effective prior conditional statements

如果结果s是unreachable则 确定是存在的隐式路径依赖，我举个小例子，帮助理解和回忆：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
y=0;
z=input();
if(z){
	y=1;
  x=2;
}

if(y){
	useless=1;
}

if(x==2){ 
	if(a==19970131){//target conditional statement
    //...
  }
}

假设original input对L13是reachable，但是mutated input是unreachable.两次的路径序列：

  • L4:true;L8:true;L12:true
  • L4:false;L8:false;L12:false

逆序比较:

  • L12不属于 ，按照验证算法，这里是L13是unreachable的，所以L12属于隐式的effective prior conditional statement

  • L8不属于 ，按照验证算法，这里L13还是reachable的，所以L8不属于隐式的effective prior conditional statement

  • L3不属于 ，按照验证算法，这里是L13是reachable的，所以L3不属于隐式的effective prior conditional statement

奇怪得到的结果却是L3不属于隐式的effective prior conditional statement,原文中的逆序比较似乎不合理？这个演算结果我没有想到。

0x01 Self Conclusion

在看Angora我就有一个疑问，关于梯度下降算法，因为无法保证目标路径分支是reachable的，所以计算梯度得到的结果是毫无意义的，在这篇文章里面给了我想要的答案，作者似乎修补了这个很重要的问题，用force的方法，保证两次走过的路径条件一样。疑问又来了，这样做的理论依据在哪呢？