自动机：DAF,NAF,正则表达式的关系
DAF 转化为正则表达式
基础理论
正则表达式: 描述一组满足特定规则的字符串 DAF: 有穷的字符串组成的集合我们称之为语言，DAF是用来描述语言的一种方式，它可以转换为等价的正则表达式。
正则表达式和DAF的具体关系：DAF是通过输入来描述状态转移的一种方式。对于整个DAF来说，从初始状态到接受状态或者终极状态对应一条正则表达式。而对于DAF中任意两个状态来说，之间的路径也是对应着一条正则表达式。为什么会这样呢？从DAF的状态转移扩展，从一个状态到另一个状态对应着一串输入字符串，而这串字符串也就是对应着满足特殊规则的正则表达式。这是我们DAF和正则表达式之前转换的基础理论。
正则表达式的基础理论： 1. 如果\(E\)和\(F\)都是正则表达式，则\(E+F\)也是正则表达式，表示\(L(E)\)和\(L(F)\)的并。也就是说， \[ E+F = L(E)\cup L(F) \] 2. 如果如果\(E\)和\(F\)都是正则表达式，则\(EF\)也是正则表达式,表示\(L(E)\)和\(L(F)\)的连接。也就是说， \[ EF = L(E)L(F) \] 3. 如果\(E\)是正则表达式，则\(E^*\)也是正则表达式，表示\(L(E)\)的闭包(closure)。也就是说 \[ E^* = cl(L(E)) \] 4. 如果\(E\)是正则表达式，则\((E)\)也是正则表达式，与\(E\)表示相同的语言。形式化地， \[ (E) = E \ \ \ \ \ L((E))=L(E) \] 5. 对于任意的正则表达式R: \[ \emptyset R = R\emptyset=\emptyset \] \[ \emptyset+R=R+\emptyset=R \]
分解问题
如果要把DAF转换为一个正则表达式，我们选择分治策略，先拆分问题： 1. 假设DAF有\(n\)个状态，状态的集合为\(\{1,2,3...n\}\) 2. 任取其中两个状态\(i\)和\(j\),先求\(i\)到\(j\)不经过其他状态路径对应的正则表达式 3. 求\(i\)到\(j\)，最高只经过状态\(1\)的路径对应的正则表达式 4. 求\(i\)到\(j\)，最高只经过状态\(2\)的路径对应的正则表达式 5. 求\(i\)到\(j\)，最高只经过状态\(3\)的路径对应的正则表达式 6. 以此类推，往下求 7. 求\(i\)到\(j\)，最高只经过状态\(n\)的路径对应的正则表达式
小疑问：
- 什么叫最高只经过状态\(k\),\(k\)属于\(\{1,2,3...n\}\)? 这里指的是从状态i到状态j路径中的状态最高不超过k。
- 状态\(i\),\(j\),\(k\)直接有什么相互的联系吗? 这里并没有必然的联系，\(i\)可以等于\(j\)，而且状态\(i\)，\(j\)可以大于\(k\)，也可以小于\(k\)。
状态\(i\)到状态\(j\)的路径:
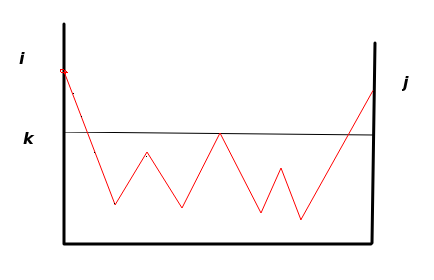垂直方向为状态，这里我们取每个顶点为某个具体的状态，线段表示状态的转移，可以看到这里虽然有2次经过了状态\(k\)，但是都是两个端点，除两个端点状态之外，并没有经过大于状态\(k\)的，状态转移。这幅图在这里表示为带有属于正则表达式\(R_{ij}^{(k)}\)的语言的标记的路径。
为了构造\(R_{ij}^{(k)}\)表达式，我们把从状态i到状态j最高只经过状态k的路径分成两种情况： 1. 根本不经过状态\(k\) 2. 至少经过一次状态\(k\)
那么对应的\(R_{ij}^{(k)}\)的表达式应该为： \[ R_{ij}^{(k)} = R_{ij}^{(k-1)} + R_{ik}^{(k-1)} (R_{kk}^{(k-1)})^* R_{kj}^{(k-1)} \]
两次情况取并集，\(R_{ij}^{(k-1)}\)好理解就是根本不经过状态\(k\)的情况，而后一种情况我们需要再次分解： 1. 状态\(i\)第一次到状态\(k\)的路径 2. 状态\(k\)到状态\(k\)的任意次路程 3. 最后状态\(k\)到状态\(j\)的路径
最后三者取正则表达式的连接组成了\(R_{ik}^{(k-1)} (R_{kk}^{(k-1)})^* R_{kj}^{(k-1)}\),这里为什么是\(k-1\),因为每种单次路径都没有大于经过k-1，除两端点以为。
结论
最终对于所有的i和j,都能得到\(R_{ij}^{(n)}\),因为上述计算\(R_{ij}^{(k)}\)过程是可以归纳成递归式。这里可以假设，状态\(1\)是初始状态，而接受状态可以是任意一组状态。自动机语言的正则表达式，就是所有表达式\(R_{1j}^{(n)}\)之和(并)，使得状态\(j\)为接受状态.
通过消除法将自动机转换为正则表达式
如图，其中\(s\)为一个一般状态。假设\(s\)以\(q_1\),\(q_2\),\(q_3\)...\(q_n\)作为s的前驱状态，以\(p_1\),\(p_2\),\(p_3\)...\(p_m\)作为s的后继状态，是可能存在\(q\)和\(p\)是相同的情况，但是假设\(s\)不出现在\(q\),\(p\)里面，\(s\)有到自身的环。在每一个从\(q\)到\(s\)的箭弧，都可以用正则表达式\(Q_i\)来表示。同样，对每一个从\(s\)到\(p\)的箭弧都可以同\(P_i\)来表示。\(s\)自身的环用\(S\)来表示。对应任意的\(q\)到\(p\)的箭弧用正则表达式\(R_{ij}\)来表示。注意里面的有些箭弧实际上是不存在的，这个时候就让这些箭弧的表达式为\(\emptyset\)
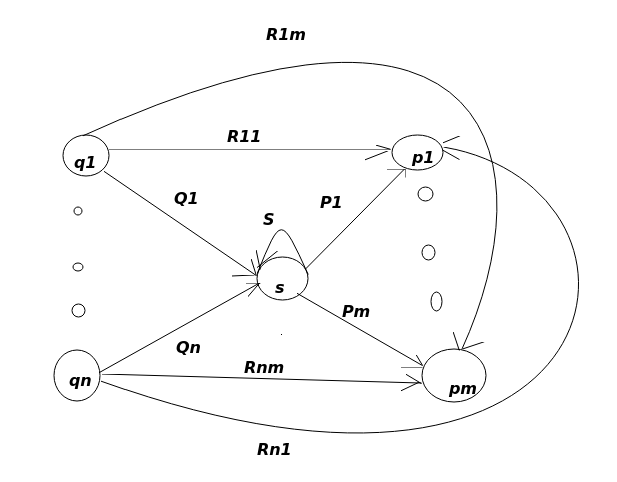
设想： 如果需要消除状态\(s\),就需要删掉所有关于\(s\)的箭弧，作为补偿，任意\(q_i\)到\(s\)，然后再从\(s\)到\(p_j\),这一过程用正则表达式\(Q_iS^*P_j\)来表示，然后把这个表达式并到\(R_{ij}\)上。
从有穷自动机构造正则表达式的策略如下：
- 对于每个接受状态\(q\),从\(q_0\)开始，消除所有中间状态，产生一个等价的自动机，所有箭弧用正则表达式来表示。最后只留下接受状态\(q\)和\(q_0\),再把所有\(q_0\)到接受状态\(q\)的正则表达式取并。
- 如果\(q\neq q_0\),最后状态图如下,其路径可以用正则表达式\((R+SU^*T)^*SU^*\),其中\((R+SU^*T)^*\)表示\(q_0\)自身环和经过\(q\)又回到\(q_0\)的环：
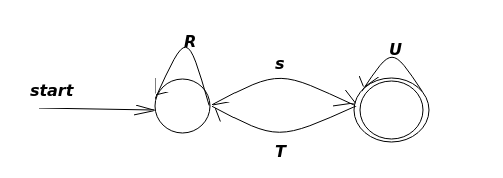
- 如果初始状态和接受状态相同，那就相当于去掉了所有状态，只留下了初始状态，只剩下一个单状态的自动机
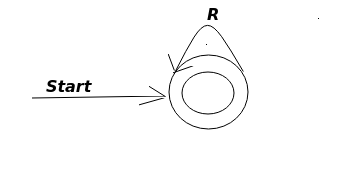
最后所有的从初始状态到接受状态的状态图都可以用上面的两幅图来表示。
对比
消除法和第一种分治法是有一定区别，分治法需要考虑所有\(q_0\)到\(q_n\)的\(k\)值。有可能原来自动机状图并不会进过某个状态\(q_k\),而消除法考虑了这一点，只会考虑其中间状态的前驱和后继状态。相对来说消除法更高效。